INTRODUCTION OF TWO-DIMENSIONAL TOMOGRAPHY FOR MONITORING THE TRANSVERSE BEAM EMITTANCES AT SIN
Urs Rohrer and Werner Joho, SIN
Tomography is a method for reconstructing a multidimensional source from a number of
selected projections. Its initial and best known applications today are in medical radiology.
The goal of two-dimensional beam tomography is the reconstruction of the probability
distribution in two-dimensional phase space from a few (at least three, one near a waist)
measured profiles. The method is non-destructive, i.e. the emittance may be monitored on line
at 120 uA (beam power 70 kW at 590 MeV).
The reconstruction is done using the computer programme MENT2A [1], which we received from
Los Alamos. The algorithm for reconstructing the distributions is designed to converge to
a solution with maximum entropy [2] or - in other words - yields an image with the lowest
information content consistent with the measured profile data. The incomplete information
concerning the beam (only a few projections) is thus supplemented by demanding that the
probability distribution has the smoothest shape permitted by the profile data [3].
The initial code was changed so that both drift-lengths and quadrupole lenses may be placed
between the profile monitors. This modification was necessary to increase the amount of
available data for firmer values of the emittances. The phase space distribution of a beam
may also be monitored by measuring profiles at the same location with different quadrupole
excitations, but the transfer matrix elements of the lenses must be well known.
At SIN, beam tomography has been tested successfully with three proton beam lines (IW1,
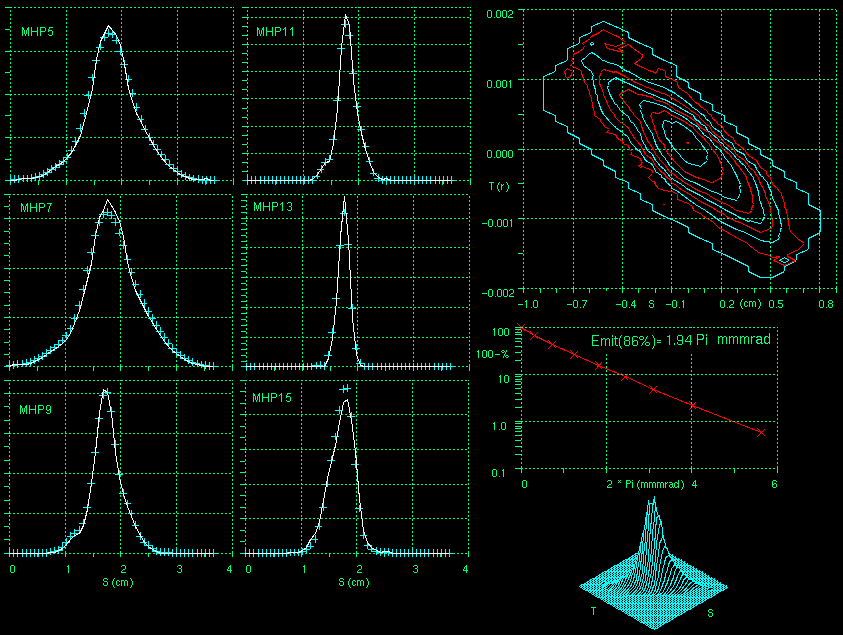
PKM and PKB) and with two pion beam lines (piE1 and uE1). Figure 1 shows results from the
590 MeV proton beam line (PKM, horizontal plane). The method of data taking using a small
dedicated computer (PDP 11/24) and that of fitting the data and producing graphical output
of the results using a more powerful computer (VAX 11/782) has been described elsewhere.
In order to avoid the formation of artifacts during the reconstruction of the phase space
distribution, two digital filters were added to the code. With the help of a fast Fourier
transform (FFT) noisy profile data may be smoothed. In addition the bandwidth of the
functions needed for the reconstruction (H-factors) may also be limited.
Computing the emittance from measured profile widths (4 sigma) with the programme TRANSPORT
[5] and comparing it with the corresponding value extracted from the log(1-f) diagram (see
Fig. 1 and Ref.[6]) shows no difference within the error (ex = 2 
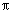mm mrad, f = 1-e-² = 0.86,
f = fraction of beam inside emittance ex). It was observed that beam tomography based on the
MENT algorithm tends to overestimate the emittances, whereas TRANSPORT tends to underestimate
them. For beam lines where the available profile data come from optically unfavorable
locations, the values extracted from the two methods may differ by a factor of two.
